jueves, 26 de noviembre de 2015
Dibujo
https://docs.google.com/presentation/d/1sHJLig7mlr8K6Cwr-ZGZZBlizJvX1UX2KFh9FT64ED8/edit?usp=sharing
miércoles, 25 de noviembre de 2015
Compuertas lógicas
Indice
1. Objetivo
2. Introducción
3. Lógica positiva
4. Lógica negativa
5. Tabla de verdad
6. Compuertas lógicas
6.1 Compuerta
AND
6.2 Compuerta
OR
6.3 Compuerta NOT
6.4 Compuerta YES o
BUFFER
7. Compuertas lógicas combinadas
7.1 Compuerta NAND
7.2 Compuerta NOR
8. Circuito lógico
9. Simplificación de circuitos
9.1 Mapa de Karnaugh
10. Resumen
11. Mapa mental
12. Conclusión
1. Objetivo
Ofrecer información útil sobre compuertas lógicas, abarcando
temas como lógica boolena y circuitos electrónicos.
2. Introducción
Dentro de la electrónica digital, existe un gran
número de problemas a resolver que se repiten normalmente. Por
ejemplo, es muy común que al diseñar un circuito electrónico necesitemos tener
el valor opuesto al de un punto determinado, o que cuando un cierto
número de pulsadores estén activados, una salida permanezca apagada. Todas
estas situaciones pueden ser expresadas mediante ceros y unos, y tratadas
mediante circuitos digitales. Los elementos básicos de cualquier circuito
digital son las compuertas lógicas. A continuación se dará a conocer más sobre
el tema de compuertas lógicas.
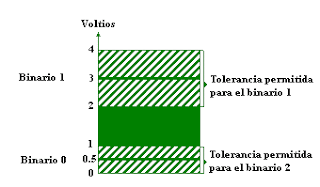
3. Lógica Positiva
En esta notación al 1 lógico le corresponde el nivel más
alto de tensión y al 0 lógico el nivel más bajo, pero que ocurre cuando la
señal no está bien definida, entonces habrá que conocer cuáles son
los límites para cada tipo de señal (conocido como tensión de
histéresis), en este gráfico se puede ver con mayor claridad
cada estado lógico y su nivel de tensión.
4. Lógica Negativa
Aquí ocurre todo lo contrario, es decir, se representa al
estado "1" con los niveles más bajos de tensión y
al "0" con los niveles más altos.
Por lo general se suele trabajar
con lógica positiva, la forma más sencilla de representar estos
estados es como se puede ver en el siguiente gráfico.
5. Tabla de verdad
Tablas de verdad o tabla de valores de verdad, es una
tabla que muestra el valor de verdad de una proposición compuesta,
para cada combinación de valores de verdad que se pueda asignar a sus
componentes.
La tabla de verdad es
un instrumento utilizado para la simplificación
de circuitos digitales a través de su ecuación booleana.
Todas las tablas de verdad funcionan de la misma manera
sin importar la cantidad de columnas que tenga
y todas tienen siempre una columna de salida (la
última columna a la derecha) que representa el resultado de todas las
posibles combinaciones de las entradas.
El número total de columnas en una tabla de
verdad es la suma de las entradas que hay + 1 (la columna de la
salida).
Verdadero
El valor verdadero se representa con la letra V; si se
emplea notación numérica se expresa con un uno: 1; en un circuito
eléctrico, el circuito está cerrado.
Falso
El valor falso se representa con la letra F; si se
emplea notación numérica se expresa con un cero: 0; en un circuito
eléctrico, el circuito está abierto.
Variable
Para una variable lógica A, B, C... que
pueden ser verdaderas V, o falsas F, los operadores fundamentales se
definen así:
Negación
La negación es un operador que se ejecuta, sobre
un único valor de verdad, devolviendo el valor contradictorio de
la proposición considerada.
Conjunción
La conjunción es un operador que actúa sobre dos
valores de verdad, típicamente los valores de verdad de dos proposiciones,
devolviendo el valor de verdad verdadero cuando ambas proposiciones
son verdaderas, y falso en cualquier otro caso. Es decir es verdadera
cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:
Hace referencia a el conector "y"
Disyunción
La disyunción es un operador que actúa sobre dos
valores de verdad, típicamente los valores de verdad de dos proposiciones,
devolviendo el valor de verdad verdadero cuando una de las
proposiciones es verdadera, o cuando ambas lo son, y falso cuando
ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:
6. Compuertas lógicas
Las computadoras digitales utilizan el sistema de números
binarios, que tiene dos dígitos 0 y 1. Un dígito binario se denomina
un bit. La información está representada en las computadoras
digitales en grupos de bits. Utilizando diversas técnicas de codificación los
grupos de bits pueden hacerse que representen no solamente números binarios
sino también otros símbolos discretos cualesquiera, tales como dígitos
decimales o letras de alfabeto. Utilizando arreglos binarios y diversas técnicas
de codificación, los dígitos binarios o grupos de bits pueden utilizarse para
desarrollar conjuntos completos de instrucciones para realizar diversos tipos
de cálculos.
La lógica binaria tiene que ver con variables binarias y con
operaciones que toman un sentido lógico. La manipulación de información binaria
se hace por circuitos lógicos que se denominan Compuertas.
La información binaria se representa en un sistema digital
por cantidades físicas denominadas señales, las señales eléctricas tales como
voltajes existen a través del sistema digital en cualquiera de dos valores
reconocibles y representan una variable binaria igual a 1 o 0. Por ejemplo, un
sistema digital particular puede emplear una señal de 3 volts para
representar el binario "1" y 0.5 volts para el binario
"0".
Las compuertas son bloques del hardware que producen señales
en binario 1 o 0 cuando se satisfacen los requisitos de entrada lógica. Las
diversas compuertas lógicas se encuentran comúnmente en sistemas de
computadoras digitales. Cada compuerta tiene un símbolo gráfico diferente y su
operación puede describirse por medio de una función algebraica. Las relaciones
entrada - salida de las variables binarias para cada compuerta pueden
representarse en forma tabular en una tabla de verdad.
A continuación se detallan los nombres, símbolos, gráficos,
funciones algebraicas, y tablas de verdad de las compuertas más usadas.
6.1 Compuerta AND
Cada compuerta tiene dos variables de entrada designadas por
A y B y una salida binaria designada por x.
La compuerta AND produce la multiplicación lógica AND: esto es: la salida es 1
si la entrada A y la entrada B están ambas en el binario 1: de otra manera, la
salida es 0.
Estas condiciones también son especificadas en la tabla de verdad para la
compuerta AND. La tabla muestra que la salida x es 1 solamente cuando ambas
entradas A y B están en 1.
El símbolo de operación algebraico de la función AND es el mismo que el símbolo
de la multiplicación de la aritmética ordinaria (*).
Las compuertas AND pueden tener más de dos entradas y por definición, la salida
es 1 si todas las entradas son 1.
6.2 Compuerta OR:
La compuerta OR produce la función sumadora, esto es, la
salida es 1 si la entrada A o la entrada B o ambas entradas son 1; de otra
manera, la salida es 0.
El símbolo algebraico de la función OR (+), es igual a la operación de
aritmética de suma.
Las compuertas OR pueden tener más de dos entradas y por definición la salida
es 1 si cualquier entrada es 1.
6.3 Compuerta NOT
El circuito NOT es un inversor que invierte el nivel lógico
de una señal binaria. Produce el NOT, o función complementaria. El símbolo
algebraico utilizado para el complemento es una barra sobra el símbolo de la
variable binaria.
Si la variable binaria posee un valor 0, la compuerta NOT cambia su estado al
valor 1 y viceversa.
El círculo pequeño en la salida de un símbolo gráfico de un inversor designa un
inversor lógico. Es decir cambia los valores binarios 1 a 0 y viceversa.
6.4 Yes o Buffer
Un símbolo triángulo por sí mismo designa un circuito
separador, el cual no produce ninguna función lógica particular puesto que el
valor binario de la salida es el mismo de la entrada.
Este circuito se utiliza simplemente para amplificación de la señal. Por
ejemplo, un separador que utiliza 5 volt para el binario 1, producirá una
salida de 5 volt cuando la entrada es 5 volt. Sin embargo, la corriente
producida a la salida es muy superior a la corriente suministrada a la entrada
de la misma.
De ésta manera, un separador puede excitar muchas otras compuertas que
requieren una cantidad mayor de corriente que de otra manera no se encontraría
en la pequeña cantidad de corriente aplicada a la entrada del separador.
7. Compuertas lógicas combinadas
Al agregar una compuerta NOT a cada una de las compuertas
anteriores los resultados de sus respectivas tablas de verdad se invierten, y
dan origen a tres nuevas compuertas llamadas NAND y NOR. Veamos ahora como son y cuál es el
símbolo que las representa...
7.1 Compuerta NAND
Es el complemento de la función AND, como se indica por el
símbolo gráfico, que consiste en una compuerta AND seguida por un pequeño
círculo (quiere decir que invierte la señal).
La designación NAND se deriva de la abreviación NOT - AND. Una designación más
adecuada habría sido AND invertido puesto que es la función AND la que se ha
invertido.
Las compuertas NAND pueden tener más de dos entradas, y la salida es siempre el
complemento de la función AND.
7.2 Compuerta NOR
La compuerta NOR es el complemento de la compuerta OR y
utiliza el símbolo de la compuerta OR seguido de un círculo pequeño (quiere
decir que invierte la señal). Las compuertas NOR pueden tener más de dos
entradas, y la salida es siempre el complemento de la función OR.
8. CIRCUITO LÓGICO
Los circuitos lógicos se forman combinando compuertas
lógicas. La salida de un
circuito lógico se obtiene combinando las tablas
correspondientes a sus compuertas
componentes.
Por ejemplo
Es fácil notar que las tablas correspondientes a las
compuertas OR, AND y NOT son
respectivamente idénticas a las tablas de verdad de la
disyunción, la conjunción y la
negación en la lógica de enunciados, donde sólo se ha
cambiado V y F por 0 y 1. Por lo
tanto, los circuitos lógicos, de los cuales tales compuertas
son elementos, forman un
álgebra de Boole al igual que los enunciados de la lógica de
enunciados.
Adoptaremos, entonces, aquí las mismas convenciones
adoptadas en el caso del
álgebra de Boole:
- Omitimos el símbolo *, usándose en su lugar la yuxtaposición de variables.
- Establecemos que + es más fuerte que * y * es más fuerte que ‾.
Puesto que tanto el álgebra de Boole es la estructura
algebraica tanto de los circuitos
como de la lógica de enunciados, la salida de un circuito
lógico también puede expresarse
en el lenguaje de la lógica de enunciados. Por ejemplo, la
salida del circuito anterior
resulta:
La salida de este circuito, expresada en el lenguaje de la
lógica de enunciados, resulta:
9. SIMPLIFICACIÓN DE CIRCUITOS
9.1 Mapa de Karnaugh
Los Mapas de Karnaugh son una herramienta muy
utilizada para la simplificación de circuitos lógicos. Cuando se tiene una
función lógica con su tabla de verdad y se desea implementar esa
función de la manera más económica posible se utiliza este método.
Ejemplo: Se tiene la siguiente tabla de verdad
para tres variables.
Se desarrolla la función lógica basada en ella. (Primera
forma canónica). Ver que en la fórmula se incluyen solamente las variables (A,
B, C) cuando F cuando es igual a "1".
Si A en la tabla de verdad es "0" se
pone A, si B = "1" se pone B, Si C = "0" se
pone C, etc.
IMAGEN IMAGEN
F = A B C + A B C +
A BC + A B C + A B C + A B C
Una vez obtenida la función lógica, se implementa
el mapa de Karnaugh.
Este mapa tiene 8 casillas que corresponden a 2n,
donde n = 3 (número de variables (A, B, C)).
La primera fila corresponde a A = 0
La segunda fila corresponde a A = 1
La primera columna corresponde a BC = 00 (B=0 y C=0)
La segunda columna corresponde a BC = 01 (B=0 y C=1)
La tercera columna corresponde a BC = 11 (B=1 y C=1)
La cuarta columna corresponde a BC = 10 (B=1 y C=0)
En el mapa de Karnaugh se
han puesto "1" en las casillas que corresponden a los
valores de F = "1" en la tabla de verdad. Tomar en cuenta
la numeración de las filas de la tabla de verdad y la numeración de
las casillas en el mapa de Karnaugh.
Para proceder con la simplificación, se crean
grupos de "1"s que tengan 1, 2, 4, 8, 16, etc.
(sólo potencias de 2). Los "1"s deben estar adyacentes (no
en diagonal) y mientras más "1"s tenga el grupo, mejor.
La función mejor simplificada es aquella que tiene el menor
número de grupos con el mayor número de "1"s en cada grupo
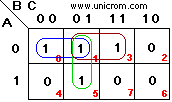
Se ve del gráfico que hay dos grupos cada uno de cuatro
"1"s, (se permite compartir casillas entre los grupos).
IMAGEN
La nueva expresión de la función booleana simplificada se
deduce del mapa de Karnaugh.
- Para el primer grupo (rojo): la simplificación da B (los
"1"s de la tercera y cuarta columna) corresponden a B sin negar)
- Para el segundo grupo (azul): la simplificación da A (los
"1"s están en la fila inferior que corresponde a A sin negar)
Entonces el resultado es F = B + A o F = A +
B
Ejemplo:
Una tabla de verdad como la de la derecha da la
siguiente función booleana:
F = A͞B͞C + A͞B C + A̅ B C +
A B̅ C
Se ve claramente que la función es un reflejo
del contenido de la tabla de verdad cuando F =
"1"
Con esta ecuación se crea el mapa de Karnaugh y
se escogen los grupos. Se lograron hacer 3 grupos de dos "1"s cada
uno.
Se puede ver que no es posible hacer grupos de 3, porque 3
no es potencia de 2. Se observa que hay una casilla que es compartida por
los tres grupos.
La función simplificada es: F = AB + AC
+ BC. Grupo en azul: AB, grupo marrón: AC, grupo verde: BC
10. RESUMEN
Las computadoras digitales utilizan el sistema de números
binarios, que tiene dos dígitos 0 y 1. Un dígito binario se denomina
un bit. La información está representada en las computadoras
digitales en grupos de bits. La manipulación de información binaria se hace por
circuitos lógicos que se denominan Compuertas.
Las compuertas son bloques del hardware que producen señales
en binario 1 o 0 cuando se satisfacen los requisitos de entrada lógica.
Cada compuerta tiene un símbolo gráfico diferente y su
operación puede describirse por medio de una función algebraica.
Las relaciones entrada - salida de las variables binarias
para cada compuerta pueden representarse en forma tabular en una tabla de
verdad.
Tablas de verdad o tabla de valores de verdad, es una
tabla que muestra el valor de verdad de una proposición compuesta,
para cada combinación de valores de verdad que se pueda asignar a sus
componentes. La tabla de verdad es un instrumento utilizado
para la simplificación de circuitos digitales a través de su ecuación
booleana.
Compuerta AND : produce la multiplicación lógica AND: esto
es: la salida es 1 si la entrada A y la entrada B están ambas en el binario 1:
de otra manera, la salida es 0.
Compuerta OR: produce la función sumadora, esto es, la
salida es 1 si la entrada A o la entrada B o ambas entradas son 1; de otra
manera, la salida es 0.
Compuerta NOT: es un
inversor que invierte el nivel lógico de una señal binaria. Si la variable
binaria posee un valor 0, la compuerta NOT cambia su estado al valor 1 y
viceversa.
Yes o Buffer: Un símbolo triángulo por sí mismo designa un circuito separador,
el cual no produce ninguna función lógica particular puesto que el valor
binario de la salida es el mismo de la entrada.
Compuerta NAND: es el complemento de la función AND,
como se indica por el símbolo gráfico, que consiste en una compuerta AND
seguida por un pequeño círculo (quiere decir que invierte la señal).
Compuerta NOR: la compuerta NOR es el complemento de la compuerta OR y
utiliza el símbolo de la compuerta OR seguido de un círculo pequeño (quiere
decir que invierte la señal). Las compuertas NOR pueden tener más de dos
entradas, y la salida es siempre el complemento de la función OR.
Los Mapas de Karnaugh son una herramienta muy
utilizada para la simplificación de circuitos lógicos. Cuando se tiene una
función lógica con su tabla de verdad y se desea implementar esa
función de la manera más económica posible se utiliza este método.
11. Mapa mental
12. CONCLUSIÓN
Se puede apreciar la importancia que toman las compuertas
lógicas dentro de la electrónica, y en nuestra vida diaria, esto debido a que
nos permiten en cierta manera controlar algunos dispositivos tecnológicos. La
gama de aplicaciones es bastante extensa debido a que su funcionamiento es
bastante fácil de comprender permitiéndonos así utiliza una gran cantidad de
compuertas en un solo circuito.
Referencias
Suscribirse a:
Comentarios (Atom)